股票市场系统特性分析及应用
股票市场系统特性分析及应用
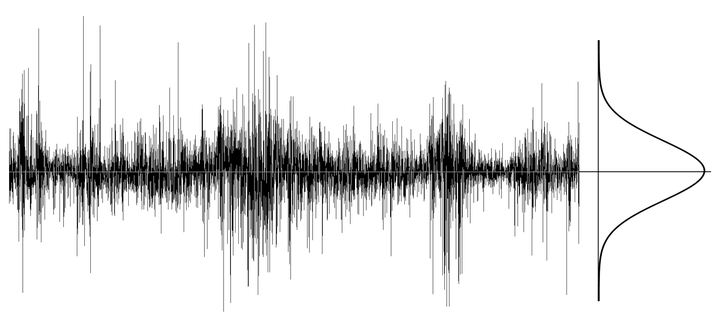
图3 上证指数收益率(日) 三)、几何布朗运动模型 Working、Kendall、Osborne、Samuelson和 Fama等人的实证研究结果也均表明:股票价格的短期收益率为白噪声序列。 设 为 时刻的股票价格,则股票价格 在 区间的收益率可表示为 式中 为服从 正态分布的白噪声时间函数, 为白噪声函数的标准差, 的物理意义代表白噪声信号在单位电阻上产生的平均功率。 式(1)也可表示为布朗运动形式 式中 为标准布朗运动随机过程 的一条样本轨道, 的一阶差分 为服从(0,1)正态分布的白噪声函数。 式(1)和式(2)是众多学者通过对股票市场长期观察和实证研究得到的经验模型,式中的 、 和 均为时间函数,或随机过程中的样本轨道。 Samuelson将式(2)中的 和 假设为随机变量 和 ,同时增加了线性漂移项,建立了著名的几何布朗运动模型 frac{dS(t)}{S(t)}=mu t+sigma dB(t) (3) 式中 为漂移率,是指单位时间内股票价格收益率均值的变化值, 为股票价格日收益率的标准差,称为波动率。 由式(3),可以求出对数股票价格 的数学期望和方差分别 表明股票价格的对数 服从方差为 的正态分布,或股票价格服从对数正态分布。 根据正态分布的对称性和集中性特征,对数股票价格 应具有如下特征: (1)对称性。对数股票价格 在均值 两侧出现的次数大致相等。 (2)集中性。大多数对数股票价格 位于均值 附近, 分布曲线的高峰位于 。 观察实际股票价格的对数,完全不符合正态分布的对称性和集中性。 事实上,式(3)的随机变量模型是描述大量样本轨道空间统计特性的数学模型,“股票价格服从对数正态分布”指的是大量样本轨道位置在任意时刻均服从正态分布的性质。 图4给出了式(3)几何布朗运动模型描述的1000条样本轨道,这1000条样本轨道在 时刻的取值服从方差为 的正态分布,显然具有正态分布的对称性和集中性特征。而实际观察到的对数股票价格 只是其中的一条样本轨道,不具有正态分布的对称性和集中性。