股票市场系统特性分析及应用
股票市场系统特性分析及应用
t时刻的空间位置服从(0,tσ2)正态分布。
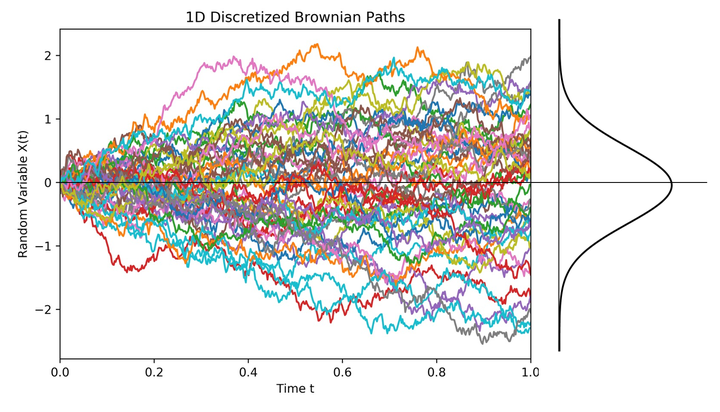
图3 布朗运动随机过程、随机变量和样本轨道 四)、结论: 股票价格只是随机过程中的一条样本轨道,也就是中学函数定义的时间函数。股票价格数学模型应该回归到式(1)或式(2)表示的时间函数模型,这样才能正确描述股票价格随机现象,并揭示股票价格运动规律。 五、为什么股票价格不服从对数正态分布? 一)、正态分布的特征: 图1为英国生物统计学家高尔顿专门设计用来演示正态分布曲线及其特征的实验模型,通常称为高尔顿板(Galton Board)。 高尔顿板上的每一个圆点表示钉在板上的钉子,钉子之间的距离彼此相等,呈三角形排列,上一层每一颗钉子的位置恰好位于下一层两颗钉子的正中间。 当小球从最上方的入口落下时,小球每次碰到钉子后向左、右两个方向落下的概率各为50%,直到最后落入底部的一个格子内。把大量小球逐个从入口处放下,只要高尔顿板的面积足够大、钉子数量足够多,落在格子内的小球将形成与正态分布曲线相似的中间高、两边低的钟形曲线。

图1 高尔顿板正态分布实验 从高尔顿板实验结果可以看出,正态分布具有如下特点: (1)对称性。落在原点左、右两侧的小球数量大致相等。 (2)集中性。大多数小球落在原
点附近的格子内,高峰位于正中央的格子。 如果按照时间顺序依次画出每个小球落到底部的横向位移 ,则会得到图2所示的白噪声函数图像。
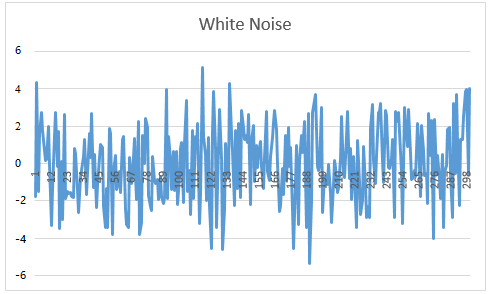
图2 高尔顿板小球位移 二)、股票价格日收益率: 图3为上证指数1998年-2020年的日收益率曲线,可以看出,上证指数的日收益率与图2所示的高尔顿板小球位移曲线相似,下一时刻收益率和小球位移的方向及大小是完全随机的,均可用白噪声时间函数进行描述。 将不同时刻的上证指数日收益率作为样本点进行统计分析,其均值为0.0002,标准差 =0.02,最大波动幅度为±0.09。上证指数的日收益率分布曲线是一条中间高,两端逐渐下降且完全对称的正态分布曲线(实际分布有尖峰厚尾现象),并具有如下的正态分布特征: (1)对称性。绝对值相等的正、负收益率出现的次数大致相等。 (2)集中性。大多数收益率位于均值附近,收益率分布曲线的高峰位于正中央。