股票市场系统特性分析及应用
股票市场系统特性分析及应用
已从随机过程的定义和基本概念角度对股票价格与时间之间的数量关系进行了分析,得出了股票价格只是随机过程中的一个样本轨道(时间函数),而非随机过程随机变量的结论。 事实上,随机过程是定义在Ω×T上的二元函数,从时间和空间两个维度描述随机现象,有时间和空间两个自变量,可用来描述大量布朗粒子随时间的空间位置分布情况。但人们观察到的股票价格变化过程只有时间一个自变量,相当于只观察一个布朗粒子的位移随时间变化过程,因此,股票价格只能被抽象为随机过程中的一条样本轨道,也就是中学函数定义的时间函数。 本文先假定股票价格为随机过程随机变量,然后推导出了一系列与事实严重不符的错误结论,从而证明了“股票价格不是随机变量”。 一)、随机游走模型 Working、Kendall、Osborne、Samuelson和 Fama等人的实证研究结果均表明:股票价格的对数收益率为零均值不相关白噪声序列。 设S(t)为t时刻的股票价格,y(t)=ln S(t),则股票价格S(t)的对数收益率可表示为 y(n)- y(n-1)=ε(n) (1) 式中ε(n)为零均值不相关白噪声时间序列。 图1为上证指数1998年-2020年的对数收益率(日),可以看出,上证指数的对数收益率与白噪声序列的函数图像极为相似,在下一时刻的方向和大小完全随机,不同时刻的对数收益率近似服从正态分布(实际分布有尖峰厚尾现象)。
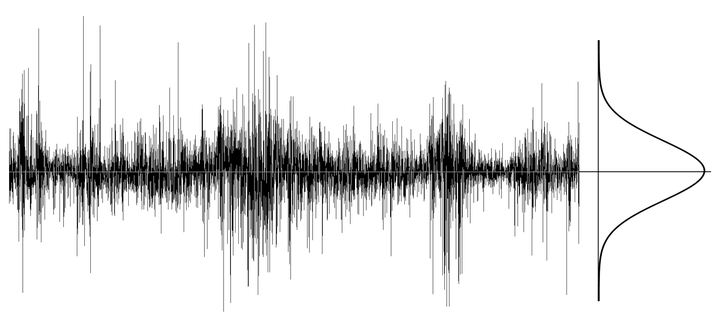
图1 上证指数对数收益率(日) 将式(1)变换为 y(n)= y(n-1)+ε(n) (2) 上式即为股票价格