t)究竟是时间t的函数？还是t时刻的随机变量？ 一）、函数定义 定义：在一个变化过程中，假设有两个变量x、y，如果对于任意一个x都有唯一确定的一个y和它对应，则称变量y为变量x的函数，记作 y=f(x) 其中变量x称为自变量，变量y称为函数。 函数f(x)通常有三种表示方法：解析法、列表法和图像法。 图1为特斯拉（NASDAQ:TSLA）股票收盘价曲线，显然为图像法表示的时间函数。对于每一个时间自变量t值，都有唯一确定的股票价格S(t)与t对应，因此，股票价格S(t)无疑是时间t的函数。    

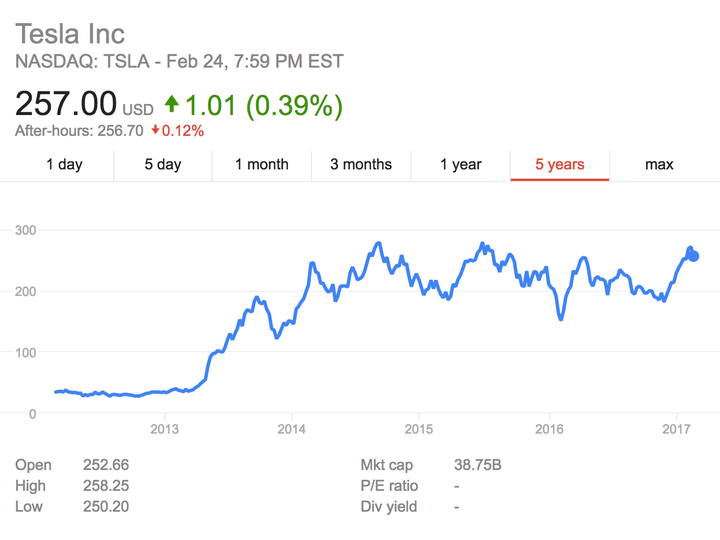
 图1 股票价格曲线 二）、随机过程、随机变量和时间函数三者之间的区别与关系  随机过程X(t)实质上是定义在Ω×T上的二元函数X（ω，t)。对于固定的时间t，X（ω，t)为状态变量ω的函数，称为随机变量，通常简记为X（t)；对于固定的ω，X（ω，t)为时间t的函数，称为样本函数或样本轨道，简记为x(t)。一个样本函数对应着随机试验中的一次“测量结果”。 图2为随机过程、随机变量和样本函数三者之间关系示意图。图中的三条样本函数曲线可分别看成是三个质点的位移时间图像，每个质点在t时刻的位置均为时间t的函数。所有质点在t时刻的空间位置（图中红点）就是随机变量在t时刻的状态。随机过程即可看成是大量随机变量的集合，也可看成是所有样本轨道的集合。

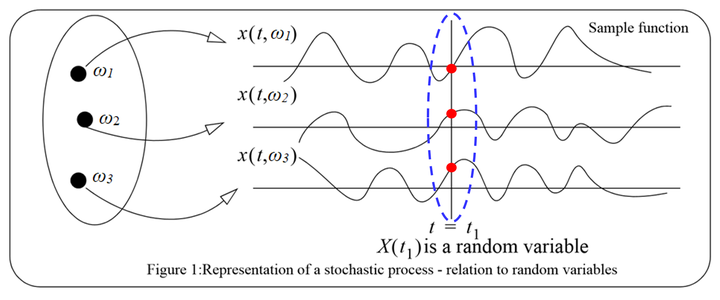
图2 随机过程、随机变量和样本函数三者之间的关系   从图2可以看出，随机变量和样本函数描述的是完全不同的实际问题。随机变量用来描述大量质点的空间统计特性，样本函数用来描述一个质点的时间运动规律。   三）、《数理金融学》的数学抽象错误： 将实际问题正确地抽象为数学问题是建立科学理论或解决实际问题的第一步（图3），也是最重要的一步。如果不能将实际问题正确地抽象为数学问题，即使使用正确的数学方法，也会得出一系列错误的结论。      

 图3 科学理论建立过程 根据随机过程的定义，图1所示的股票价格曲线，显然就是随机过程样本空间中的一条样本轨道，亦即时间函数。但是《数理金融学》却将股票价格错误地抽象为随机变量，无形中将研究对象从