股票市场系统特性分析及应用
股票市场系统特性分析及应用
随机游走模型。 注意:式(2)的随机游走模型是众多学者通过对股票价格波动现象长期观察和实证研究得到的经验模型,式中的y(n)和ε(n)均为时间的函数。 二)、反证法证明 假设式(2)随机游走模型中的y(n)和ε(n)均为随机变量,《数理金融学》和《随机过程》教科书事实上就是这样假设的。 设y(0)=0,ε(n)为服从(0,σ2)正态分布的高斯白噪声随机变量,则股票价格y(n)的数学期望和方差分别为 E[y(n)]=0 (3) D[ y(n) ]=tσ2 (4) 式(3)和式(4)表明,股票价格y(n)服从(0,tσ2)正态分布。 (1)y(n)的数学期望为零,表明股票价格中不存在长期线性趋势,Fama根据这个结论建立了著名的EMH(Efficient Markets Hypothesis)有效市场假说,得出了股票市场不可预测的结论。但是y(n)数学期望为零的结论与实际股票价格中存在长期线性趋势的事实完全不符,为了使随机变量形式的随机游走模型能够描述长期线性趋势,Samuelson强行加入了线性漂移项,建立了著名的几何布朗运动模型,但该模型的对数收益率为常数,与“股票价格的对数收益率为零均值不相关白噪声序列”的实证研究结果严重不符。 (2)y(n)的方差与时间成正比,表明股票价格中高频噪声的平均功率随时间线性增大,但实际股票价格中高频噪声的平均功率始终基本不变(见图1)。 (3)正态分布的股票价格y(n)曲线应具有正态分布的对称性和集中性,但实际股票价格曲线完全不满足正态分布的对称性和集中性。 图2给出了服从(0,tσ2)正态分布的股票价格曲线,虽然完全满足正态分布的对称性和集中性,但与实际股票价格曲线相距甚远。
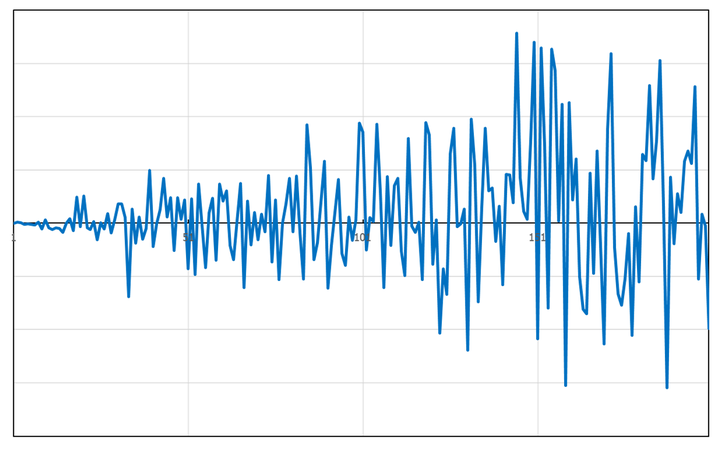
图2 服从(0,tσ2)正态分布的股票价格曲线 事实上,随机变量模型描述的是随机过程大量样本轨道的空间分布特性。 图3给出了布朗运动的随机变量和样本轨道,每条样本轨道代表每个布朗粒子的位移时间曲线,随机过程是所有样本轨道的集合,随机变量描述的是某一时刻所有样本轨道在空间的分布情况,即所有布朗粒子在