一、股票市场系统特性分析及应用 股票市场是一个由众多生命或生命群体组成的复杂巨系统,其运行状态具有明显的非线性和复杂性特点。本文采用系统科学原理和分析方法建立了股票市场系统模型,给出了股票市场的非线性、自激振荡、正反馈、有界性和初值敏感等系统特性,并对证券投资领域常用的基本分析和技术分析方法进行了对比,从系统分析角度看,技术分析考虑了引起股票价格变化的所有原因,因而技术分析是一种比基本分析更加科学、准确、可靠、有效的股票价格分析方法。
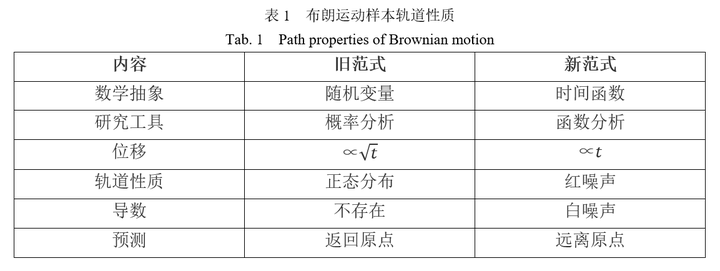
二、随机过程理论的范式危机与变革 随机过程理论是研究动态随机现象空间统计特性和时间演变规律的应用数学理论。本文首先分析了随机过程理论与经验事实不符、在逻辑上不能自洽而出现悖论、与统计物理学理论不一致,以及在金融市场的广泛应用导致金融危机等反常现象和问题,并指出随机过程理论将样本轨道假设为随机变量的研究方法,是导致随机过程理论产生范式危机的根本原因。随机过程理论必须要抛弃原有的随机变量研究范式,全面转换到新的时间函数研究范式,并用新范式重建随机过程样本轨道理论,才能正确描述并解释随机现象随时间的演变过程,为自然科学、工程技术和社会科学解决实际问题提供正确的方法、工具和理论。
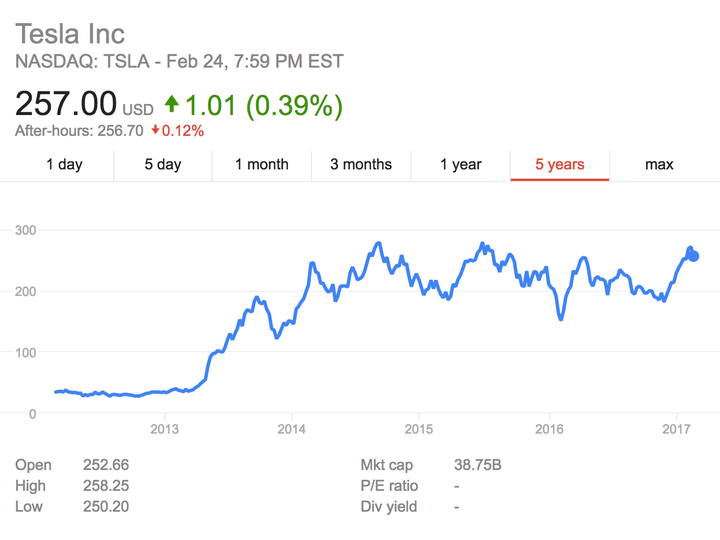
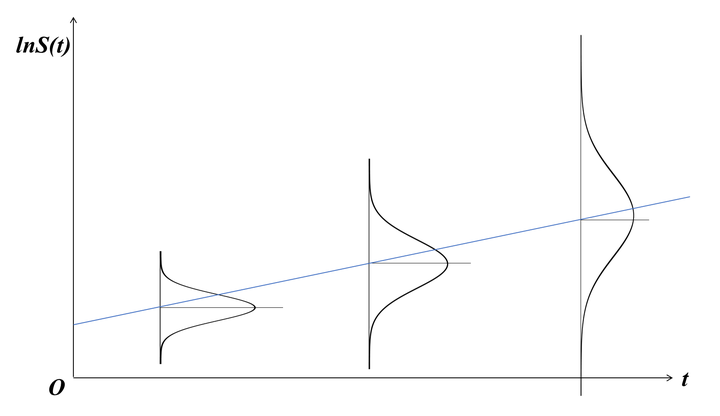
三、股票价格可预测性证明 有效市场理论认为股票的未来价格与当前和过去的历史价格无关,并得出了股票价格在统计上无记忆性、股票价格不存在趋势、股票价格无法预测和技术分析无效等一系列结论。但是大量的金融市场异象和投资实践表明,股票价格在一定程度上是可以预测的。本文根据股票价格对数收益率为不相关白噪声的实证研究结果,推导出了股票价格的自相关函数、功率谱密度及波动范围,发现了隐藏在股票价格中的长期线性趋势和低频波动,从理论上证明了在微观上表现出随机性和不可预测性的股票价格波动,在宏观上具有总体的确定性和可预测性,并给出了股票价格中低频波动的分析方法。 四、为什么股票价格不是随机变量? 问题:设S(t)为t时刻的股票价格,S(t)究竟是时间t的函数?还是t时刻的随机变量? 一)、函数定义 定义:在一个变化过程中,假设有两个变量x、y,如果对于任意一个x都有唯一确定的一个y和它对应,则称变量y为变量x的函数,记作 y=f(x) 其中变量x称为自变量,变量y称为函数。 函数f(x)通常有三种表示方法:解析法、列表法和图像法。 图1为特斯拉(NASDAQ:TSLA)股票收盘价曲线,显然为图像法表示的时间函数。对于每一个时间自变量t值,都有唯一确定的股票价格S(t)与t对应,因此,股票价格S(t)无疑是时间t的函数。
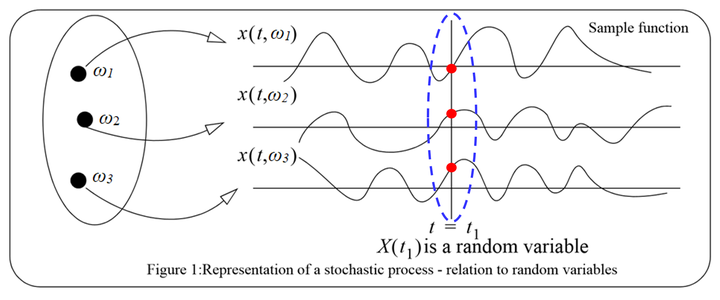
图1 股票价格曲线 二)、随机过程、随机变量和时间函数三者之间的区别与关系 随机过程X(t)实质上是定义在Ω×T上的二元函数X(ω,t)。对于固定的时间t,X(ω,t)为状态变量ω的函数,称为随机变量,通常简记为X(t);对于固定的ω,X(ω,t)为时间t的函数,称为样本函数或样本轨道,简记为x(t)。一个样本函数对应着随机试验中的一次“测量结果”。 图2为随机过程、随机变量和样本函数三者之间关系示意图。图中的三条样本函数曲线可分别看成是三个质点的位移时间图像,每个质点在t时刻的位置均为时间t的函数。所有质点在t时刻的空间位置(图中红点)就是随机变量在t时刻的状态。随机过程即可看成是大量随机变量的集合,也可看成是所有样本轨道的集合。
图2 随机过程、随机变量和样本函数三者之间的关系 从图2可以看出,随机变量和样本函数描述的是完全不同的实际问题。随机变量用来描述大量质点的空间统计特性,样本函数用来描述一个质点的时间运动规律。 三)、《数理金融学》的数学抽象错误: 将实际问题正确地抽象为数学问题是建立科学理论或解决实际问题的第一步(图3),也是最重要的一步。如果不能将实际问题正确地抽象为数学问题,即使使用正确的数学方法,也会得出一系列错误的结论。
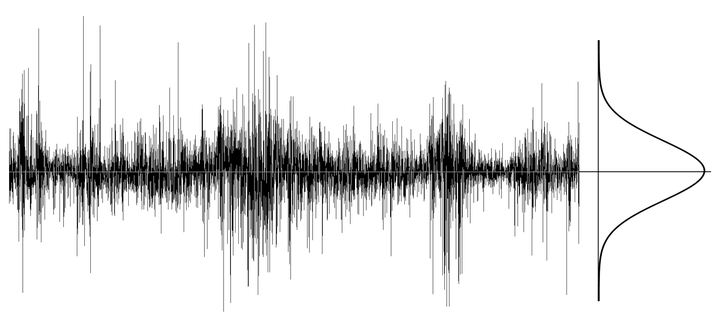
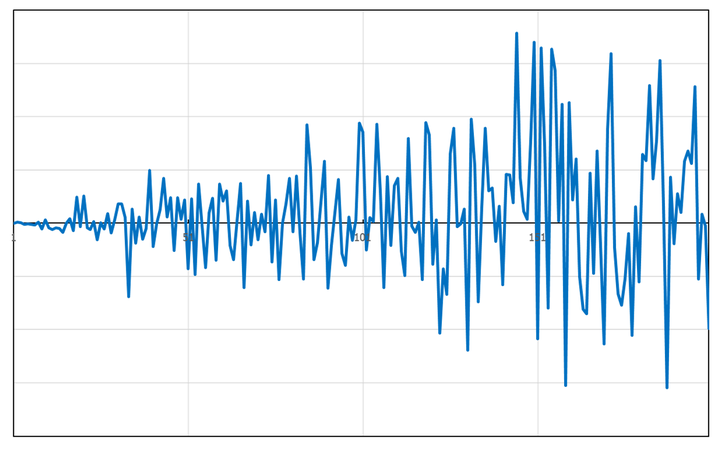
图3 科学理论建立过程 根据随机过程的定义,图1所示的股票价格曲线,显然就是随机过程样本空间中的一条样本轨道,亦即时间函数。但是《数理金融学》却将股票价格错误地抽象为随机变量,无形中将研究对象从一条样本轨道改变为大量样本轨道的集合,导致整个《数理金融学》理论建立在错误的数学抽象基础上,并用描述大量样本轨道统计规律的数字特征来刻画一条样本轨道随时间演变的规律,必然会得出一系列与事实不符的错误结论,无法正确描述并解释股票价格波动现象及规律。 四)、BS期权定价公式成为导致金融危机的主要原因 《数理金融学》理论将股票价格错误地抽象为随机变量,导致建立的股票价格模型必然无法正确描述股票价格波动现象并预测其变化趋势,在实际应用时给金融市场带来巨大的灾难。 1973年,Black和Scholes基于随机变量假设推导出了著名的BS期权定价公式,由于从理论上解决了金融衍生产品的定价问题,BS期权定价公式对华尔街各种金融创新工具和金融创新产品的面世起到了重大推动作用,使华尔街金融市场获得了空前规模的发展。但是令人意外的是,BS期权定价公式在金融市场的大规模应用,竟成为直接导致1987、1997和2007年三次重大金融危机的关键原因。人们开始怀疑《数理金融学》理论究竟能否描述或解释金融市场的波动现象和演变规律,《数理金融学》面临严峻的危机和挑战。 畅销书《黑天鹅》作者纳西姆·塔勒布在《金融时报》上发表了题为“破坏市场的伪科学”专栏文章,对数理金融学理论进行了严厉的批判,我们从一次又一次的金融危机中得出一个结论:现代数理金融学理论的有效性与占星术一样不靠谱,数理金融学理论获得诺贝尔奖不仅仅是对科学的侮辱,数理金融学理论通过创造风险来危害金融系统,一直使金融体系面临崩溃的风险。 畅销书《致命数字》作者、全球顶级金融专家特里亚纳(Triana)在《教鸟儿飞行:量化模型是否会摧毁金融市场》一书中,不仅对数理金融学理论及数学模型存在的问题进行了全面的解读,而且也严厉批判了华尔街盲目迷信数理金融学数学模型,而不相信市场趋势的模型使用方式。特里亚纳从大量的金融市场案例分析中得出结论:BS期权定价公式是金融危机的罪魁祸首,数理金融学在金融领域的应用是失败的,金融工程应该为人类历史上最严重的金融危机负责。 五、反证法证明股票价格不是随机变量 问题:假设S(t)为t时刻的股票价格,S(t)究竟是时间t的函数?还是t时刻的随机变量? 为什么股票价格不是随机变量?已从随机过程的定义和基本概念角度对股票价格与时间之间的数量关系进行了分析,得出了股票价格只是随机过程中的一个样本轨道(时间函数),而非随机过程随机变量的结论。 事实上,随机过程是定义在Ω×T上的二元函数,从时间和空间两个维度描述随机现象,有时间和空间两个自变量,可用来描述大量布朗粒子随时间的空间位置分布情况。但人们观察到的股票价格变化过程只有时间一个自变量,相当于只观察一个布朗粒子的位移随时间变化过程,因此,股票价格只能被抽象为随机过程中的一条样本轨道,也就是中学函数定义的时间函数。 本文先假定股票价格为随机过程随机变量,然后推导出了一系列与事实严重不符的错误结论,从而证明了“股票价格不是随机变量”。 一)、随机游走模型 Working、Kendall、Osborne、Samuelson和 Fama等人的实证研究结果均表明:股票价格的对数收益率为零均值不相关白噪声序列。 设S(t)为t时刻的股票价格,y(t)=ln S(t),则股票价格S(t)的对数收益率可表示为 y(n)- y(n-1)=ε(n) (1) 式中ε(n)为零均值不相关白噪声时间序列。 图1为上证指数1998年-2020年的对数收益率(日),可以看出,上证指数的对数收益率与白噪声序列的函数图像极为相似,在下一时刻的方向和大小完全随机,不同时刻的对数收益率近似服从正态分布(实际分布有尖峰厚尾现象)。
图1 上证指数对数收益率(日) 将式(1)变换为 y(n)= y(n-1)+ε(n) (2) 上式即为股票价格随机游走模型。 注意:式(2)的随机游走模型是众多学者通过对股票价格波动现象长期观察和实证研究得到的经验模型,式中的y(n)和ε(n)均为时间的函数。 二)、反证法证明 假设式(2)随机游走模型中的y(n)和ε(n)均为随机变量,《数理金融学》和《随机过程》教科书事实上就是这样假设的。 设y(0)=0,ε(n)为服从(0,σ2)正态分布的高斯白噪声随机变量,则股票价格y(n)的数学期望和方差分别为 E[y(n)]=0 (3) D[ y(n) ]=tσ2 (4) 式(3)和式(4)表明,股票价格y(n)服从(0,tσ2)正态分布。 (1)y(n)的数学期望为零,表明股票价格中不存在长期线性趋势,Fama根据这个结论建立了著名的EMH(Efficient Markets Hypothesis)有效市场假说,得出了股票市场不可预测的结论。但是y(n)数学期望为零的结论与实际股票价格中存在长期线性趋势的事实完全不符,为了使随机变量形式的随机游走模型能够描述长期线性趋势,Samuelson强行加入了线性漂移项,建立了著名的几何布朗运动模型,但该模型的对数收益率为常数,与“股票价格的对数收益率为零均值不相关白噪声序列”的实证研究结果严重不符。 (2)y(n)的方差与时间成正比,表明股票价格中高频噪声的平均功率随时间线性增大,但实际股票价格中高频噪声的平均功率始终基本不变(见图1)。 (3)正态分布的股票价格y(n)曲线应具有正态分布的对称性和集中性,但实际股票价格曲线完全不满足正态分布的对称性和集中性。 图2给出了服从(0,tσ2)正态分布的股票价格曲线,虽然完全满足正态分布的对称性和集中性,但与实际股票价格曲线相距甚远。
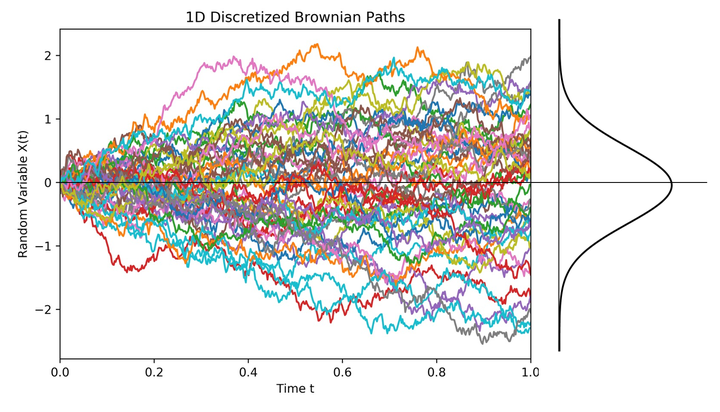
图2 服从(0,tσ2)正态分布的股票价格曲线 事实上,随机变量模型描述的是随机过程大量样本轨道的空间分布特性。 图3给出了布朗运动的随机变量和样本轨道,每条样本轨道代表每个布朗粒子的位移时间曲线,随机过程是所有样本轨道的集合,随机变量描述的是某一时刻所有样本轨道在空间的分布情况,即所有布朗粒子在t时刻的空间位置服从(0,tσ2)正态分布。
图3 布朗运动随机过程、随机变量和样本轨道 四)、结论: 股票价格只是随机过程中的一条样本轨道,也就是中学函数定义的时间函数。股票价格数学模型应该回归到式(1)或式(2)表示的时间函数模型,这样才能正确描述股票价格随机现象,并揭示股票价格运动规律。 五、为什么股票价格不服从对数正态分布? 一)、正态分布的特征: 图1为英国生物统计学家高尔顿专门设计用来演示正态分布曲线及其特征的实验模型,通常称为高尔顿板(Galton Board)。 高尔顿板上的每一个圆点表示钉在板上的钉子,钉子之间的距离彼此相等,呈三角形排列,上一层每一颗钉子的位置恰好位于下一层两颗钉子的正中间。 当小球从最上方的入口落下时,小球每次碰到钉子后向左、右两个方向落下的概率各为50%,直到最后落入底部的一个格子内。把大量小球逐个从入口处放下,只要高尔顿板的面积足够大、钉子数量足够多,落在格子内的小球将形成与正态分布曲线相似的中间高、两边低的钟形曲线。
图1 高尔顿板正态分布实验 从高尔顿板实验结果可以看出,正态分布具有如下特点: (1)对称性。落在原点左、右两侧的小球数量大致相等。 (2)集中性。大多数小球落在原
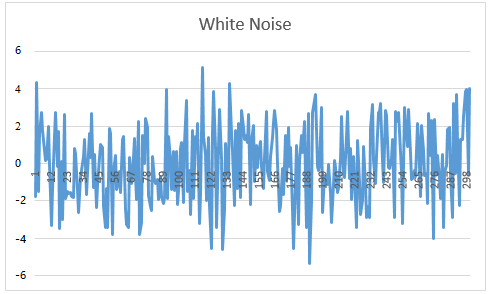
点附近的格子内,高峰位于正中央的格子。 如果按照时间顺序依次画出每个小球落到底部的横向位移 ,则会得到图2所示的白噪声函数图像。
图2 高尔顿板小球位移 二)、股票价格日收益率: 图3为上证指数1998年-2020年的日收益率曲线,可以看出,上证指数的日收益率与图2所示的高尔顿板小球位移曲线相似,下一时刻收益率和小球位移的方向及大小是完全随机的,均可用白噪声时间函数进行描述。 将不同时刻的上证指数日收益率作为样本点进行统计分析,其均值为0.0002,标准差 =0.02,最大波动幅度为±0.09。上证指数的日收益率分布曲线是一条中间高,两端逐渐下降且完全对称的正态分布曲线(实际分布有尖峰厚尾现象),并具有如下的正态分布特征: (1)对称性。绝对值相等的正、负收益率出现的次数大致相等。 (2)集中性。大多数收益率位于均值附近,收益率分布曲线的高峰位于正中央。
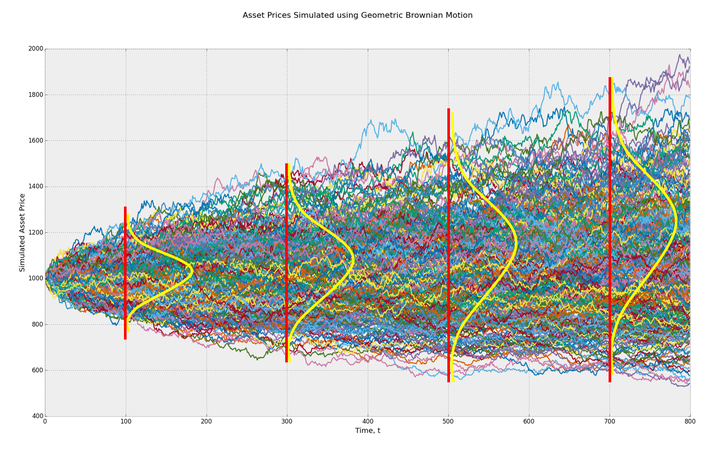
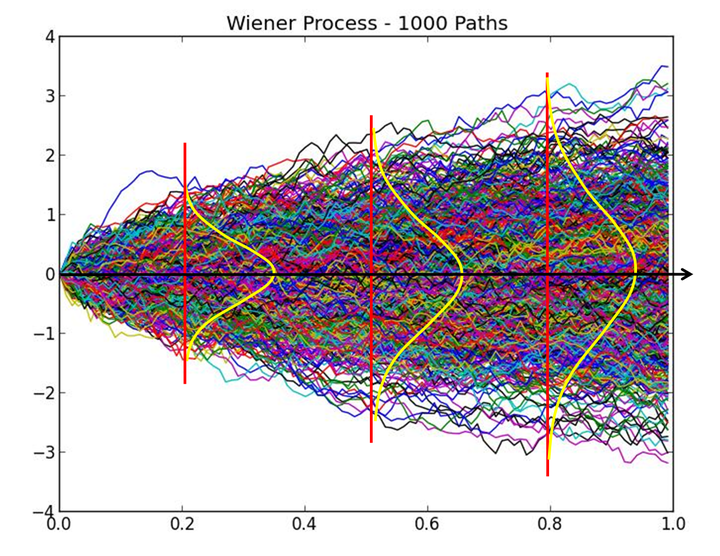
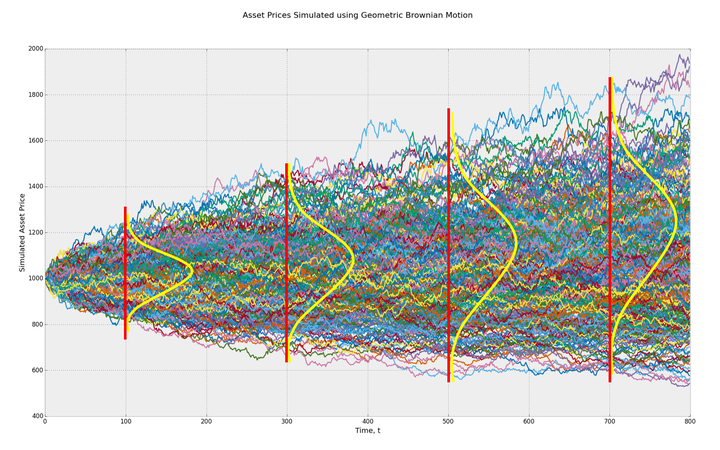
图3 上证指数收益率(日) 三)、几何布朗运动模型 Working、Kendall、Osborne、Samuelson和 Fama等人的实证研究结果也均表明:股票价格的短期收益率为白噪声序列。 设 为 时刻的股票价格,则股票价格 在 区间的收益率可表示为 式中 为服从 正态分布的白噪声时间函数, 为白噪声函数的标准差, 的物理意义代表白噪声信号在单位电阻上产生的平均功率。 式(1)也可表示为布朗运动形式 式中 为标准布朗运动随机过程 的一条样本轨道, 的一阶差分 为服从(0,1)正态分布的白噪声函数。 式(1)和式(2)是众多学者通过对股票市场长期观察和实证研究得到的经验模型,式中的 、 和 均为时间函数,或随机过程中的样本轨道。 Samuelson将式(2)中的 和 假设为随机变量 和 ,同时增加了线性漂移项,建立了著名的几何布朗运动模型 frac{dS(t)}{S(t)}=mu t+sigma dB(t) (3) 式中 为漂移率,是指单位时间内股票价格收益率均值的变化值, 为股票价格日收益率的标准差,称为波动率。 由式(3),可以求出对数股票价格 的数学期望和方差分别 表明股票价格的对数 服从方差为 的正态分布,或股票价格服从对数正态分布。 根据正态分布的对称性和集中性特征,对数股票价格 应具有如下特征: (1)对称性。对数股票价格 在均值 两侧出现的次数大致相等。 (2)集中性。大多数对数股票价格 位于均值 附近, 分布曲线的高峰位于 。 观察实际股票价格的对数,完全不符合正态分布的对称性和集中性。 事实上,式(3)的随机变量模型是描述大量样本轨道空间统计特性的数学模型,“股票价格服从对数正态分布”指的是大量样本轨道位置在任意时刻均服从正态分布的性质。 图4给出了式(3)几何布朗运动模型描述的1000条样本轨道,这1000条样本轨道在 时刻的取值服从方差为 的正态分布,显然具有正态分布的对称性和集中性特征。而实际观察到的对数股票价格 只是其中的一条样本轨道,不具有正态分布的对称性和集中性。
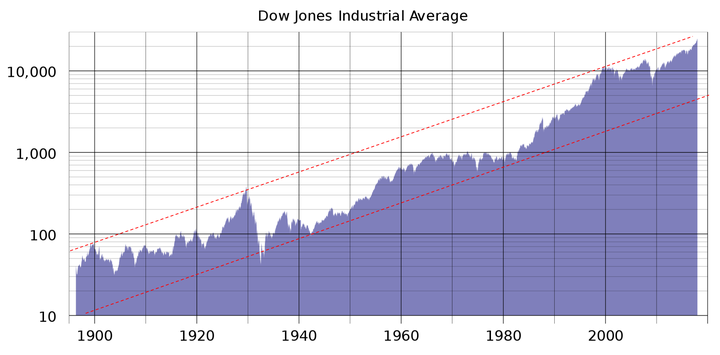
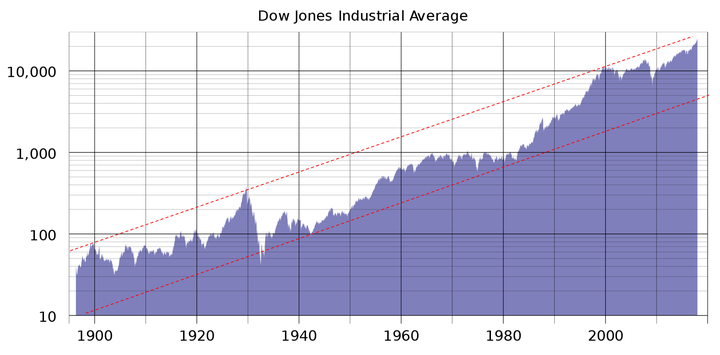
图4 几何布朗运动随机过程 四)、股票价格波动范围 图5为道琼斯工业平均指数的对数价格曲线,100多年来始终在固定宽度的线性通道范围内波动运行。股票价格可预测性证明从式(1)的时间函数模型出发,从理论上也证明了对数股票价格在线性通道内运行的结论。 图5 道琼斯工业平均指数 如果股票价格服从对数正态分布,则 时刻对数股票价格 的方差为 ,表明 在 范围内波动的概率为99.73%,这表明对数股票价格 的波动范围会随时间 的平方根不断增大,与图4几何布朗运动样本轨道的扩散范围一致,与实际对数股票价格在固定宽度的线性通道内运行的事实完全不符。因此,实际股票价格的波动范围与几何布朗运动模型的波动范围完全不同。 五、波动率的本质含义 期权定价理论首先假设股票价格服从对数正态分布,然后将(3)几何布朗运动模型的参数 定义为波动率,并用 来度量股票价格 的波动程度。 (1)标准差是用来度量随机变量样本总体偏离均值程度的数字特征。 (2)波动率 实质上是图3所示股票价格 日收益率的标准差,反映了股票价格在某一区间的日收益率偏离均值的程度。 (3)方差 是度量图4所示 (大量样本轨道)偏离均值程度的统计参数,不能用来度量一条样本轨道的波动程度。 六)、结论 股票价格服从对数正态分布的结论是基于股票价格为随机变量的假设推导出来的,《为什么股票价格不是随机变量?》和《反证法证明股票价格不是随机变量》两篇文章已分别用随机过程的定义和反证法证明了股票价格不是随机变量,而是非平稳随机过程的一条样本轨道,因此,股票价格不服从对数正态分布。 七、为什么波动率不能度量股票价格波动程度? 波动率(Volatility)是期权定价理论中度量金融资产价格波动程度的一个统计参数,对于量化分析、投资决策、资产定价、最优配置、风险管理及市场监管具有相当重要的意义。 一、布朗运动扩散系数: 1827 年,英国植物学家布朗使用显微镜观察悬浮在液体中的花粉微粒时,发现微粒总是在做无规则的运动。后来人们发现,这是一种广泛存在于自然界、工程技术和人类社会中的动态随机现象。 1905年,爱因斯坦首先使用概率分析方法对布朗运动进行了定量研究,并从热分子运动扩散方程推导出了大量一维布朗粒子位置 在 时刻的概率密度函数。 式中 为扩散系数。 从式(1)可以看出,大量一维布朗粒子在 时刻的位置服从均值为零、方差为 的正态分布,扩散系数 可用来描述大量布朗粒子偏离原点的扩散速度。 1923年,维纳根据式(1)的爱因斯坦布朗运动物理模型,归纳总结出了布朗运动的数学定义。 定义:设{ , ≥0}为随机过程,如果 (1){ , ≥0}为平稳独立增量过程; (2) ; (3)对任意的 , 服从参数为 的正态分布,其中 为常数。 则称 是参数为 的布朗运动,或维纳过程。当 时,称 为标准布朗运动,记为 。 显然,维纳过程的方差为 随机过程的标准差 是用来刻画随机变量偏离均值分散程度的数字特征,度量的是大量样本轨道偏离均值的发散程度,其物理意义与扩散系数 相同。 图1为1000个一维布朗粒子的位移曲线,这1000个布朗粒子在 时刻的位置就是随机变量 的状态, 服从参数为 的正态分布, 描述了大量布朗粒子偏离原点的扩散速度。
图1 布朗运动 标准差 不仅能度量大量布朗粒子偏离均值的发散程度,还能给出大量布朗粒子(样本轨道)位于 、 和 范围内的概率分别为68.3%、95.4%和99.7%。 图2为一个布朗粒子位移曲线的微分(瞬时速度),为服从 正态分布的高斯白噪声。因此,标准差 也可用来度量一个布朗粒子瞬时速度的大小。
图2 布朗粒子瞬时速度 二)、波动率定义 图3为上证指数的日收益率,与图2所示的布朗粒子瞬时速度完全相似,为白噪声序列。将不同时刻的上证指数对数收益率作为样本点进行统计分析,其均值为0.0002,标准差 =0.02,最大波动幅度为±0.09,近似服从正态分布。
图3 上证指数收益率(日) 期权定价理论根据股票价格的收益率为白噪声序列的实证研究结果,建立了下面的下面的几何布朗运动模型 式中 为 时刻的股票价格, 为漂移率, 为波动率。 注意:期权定价理论错误地将股票价格 假设为随机变量,从式(3)的几何布朗运动模型得出了对数股票价格 服从正态分布的结论, 的方差为 期权定价理论将股票价格日收益率的标准差 定义为股票价格波动率,可根据式(4)计算出未来 时刻的股票价格波动程度 式中 为 时刻的股票价格波动率。 例如,上证指数日收益率的标准差 =0.02,按1年250个交易日计算,上证指数的年波动率(标准差)约为32%,也就是说,上证指数一年内在 %范围内波动的概率为68.3%,在 %范围内波动的概率为95.4%,在 %范围内波动的概率为99.7%。 三、波动范围与事实不符 根据式(5)的波动率计算公式,股票价格 未来 时刻在 范围内波动的概率为99.73%,这表明对数股票价格 的波动范围会随时间 的平方根不断增大,即 的波动范围会越来越大(图4)。
图4 波动率定义的股票价格波动范围 图5为道琼斯工业平均指数的对数价格曲线,100多年来始终在固定宽度的线性通道范围内波动运行。股票价格可预测性证明从“股票价格收益率为白噪声序列”的实证研究结果出发,也推导出了对数股票价格在线性通道内运行的结论。 图5 道琼斯工业平均指数 根据波动率定义推导出的“股票价格波动范围与时间 的平方根成正比”的结论,与实际股票价格在线性通道内运行的观察结果严重不符。 四、波动率的物理意义 期权定价理论将 视为服从正态分布的随机变量,则 可用维纳过程进行描述,波动率 就是维纳过程的标准差,与布朗运动扩散系数 具有相同的物理意义,是度量大量布朗粒子扩散速度或大量样本轨道偏离均值程度的数字特征,不能用来度量一个布朗粒子位移曲线或一条样本轨道的波动程度。 五、波动率的度量对象错位 期权定价理论将股票价格假设为随机变量,因而只能用描述随机变量偏离均值程度的标准差(波动率)来度量股票价格的波动程度,无形中使波动率的度量对象从一条样本轨道改变为大量样本轨道的集合,因此,波动率无法正确度量实际股票价格的波动程度。 图6是式(3)几何布朗运动模型描述的随机过程,股票价格只是其中的一条样本轨道。波动率描述的是所有样本轨道相对均值的发散程度,而不是一条样本轨道的波动程度。