股票市场系统特性分析及应用
股票市场系统特性分析及应用
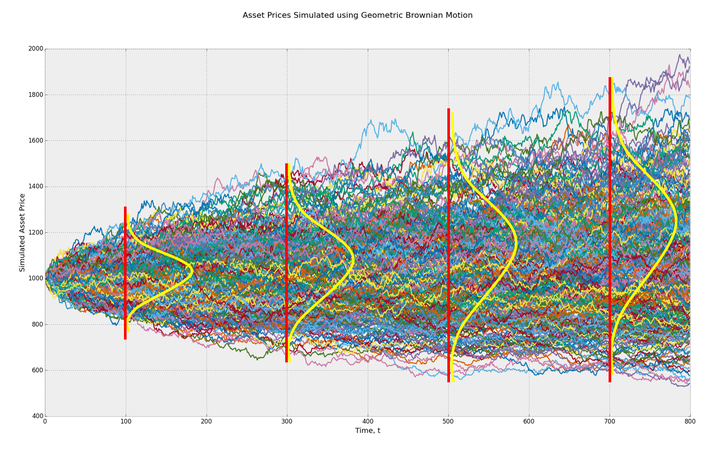
图4 几何布朗运动随机过程 四)、股票价格波动范围 图5为道琼斯工业平均指数的对数价格曲线,100多年来始终在固定宽度的线性通道范围内波动运行。股票价格可预测性证明从式(1)的时间函数模型出发,从理论上也证明了对数股票价格在线性通道内运行的结论。
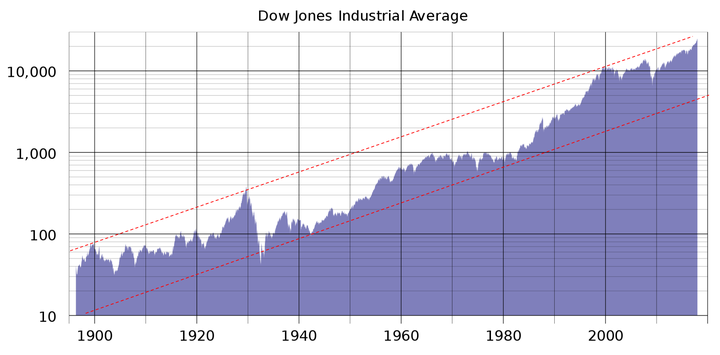
图5 道琼斯工业平均指数 如果股票价格服从对数正态分布,则 时刻对数股票价格 的方差为 ,表明 在 范围内波动的概率为99.73%,这表明对数股票价格 的波动范围会随时间 的平方根不断增大,与图4几何布朗运动样本轨道的扩散范围一致,与实际对数股票价格在固定宽度的线性通道内运行的事实完全不符。因此,实际股票价格的波动范围与几何布朗运动模型的波动范围完全不同。 五、波动率的本质含义 期权定价理论首先假设股票价格服从对数正态分布,然后将(3)几何布朗运动模型的参数 定义为波动率,并用 来度量股票价格 的波动程度。 (1)标准差是用来度量随机变量样本总体偏离均值程度的数字特征。 (2)波动率 实质上是图3所示股票价格 日收益率的标准差,反映了股票价格在某一区间的日收益率偏离均值的程度。 (3)方差 是度量图4所示 (大量样本轨道)偏离均值程度的统计参数,不能用来度量一条样本轨道的波动程度。 六)、结论 股票价格服从对数正态分布的结论是基于股票价格为随机变量的假设推导出来的,《为什么股票价格不是随机变量?》和《反证法证明股票价格不是随机变量》两篇文章已分别用随机过程的定义和反证法证明了股票价格不是随机变量,而是非平稳随机过程的一条样本轨道,因此,股票价格不服从对数正态分布。 七、为什么波动率不能度量股票价格波动程度? 波动率(Volatility)是期权定价理论中度量金融资产价格波动程度的一个统计参数,对于量化分析、投资决策、资产定价、最优配置、风险管理及市场监管具有相当重要的意义。 一、布朗运动扩散系数: 1827 年,英国植物学家布朗使用显微镜观察悬浮在液体中的花粉微粒时,发现微粒总是在做无规则的运动。后来人们发现,这是一种广泛存在于自然界、工程技术和人类社会中的动态随机现象。 1905年,爱因斯坦首先使用概率分析方法对布朗运动进行了定量研究,并从热分子运动扩散方程推导出了大量一维布朗粒子位置 在 时刻的概率密度函数。 式中 为扩散系数。 从式(1)可以看出,大量一维布朗粒子在 时刻的位置服从均值为零、方差为 的正态分布,扩散系数 可用来描述大量布朗粒子偏离原点的扩散速度。 1923年,维纳根据式(1)的爱因斯坦布朗运动物理模型,归纳总结出了布朗运动的数学定义。 定义:设{ , ≥0}为随机过程,如果 (1){ , ≥0}为平稳独立增量过程; (2) ; (3)对任意的 , 服从参数为 的正态分布,其中 为常数。 则称 是参数为 的布朗运动,或维纳过程。当 时,称 为标准布朗运动,记为 。 显然,维纳过程的方差为 随机过程的标准差 是用来刻画随机变量偏离均值分散程度的数字特征,度量的是大量样本轨道偏离均值的发散程度,其物理意义与扩散系数 相同。 图1为1000个一维布朗粒子的位移曲线,这1000个布朗粒子在 时刻的位置就是随机变量 的状态, 服从参数为 的正态分布, 描述了大量布朗粒子偏离原点的扩散速度。