股票市场系统特性分析及应用
股票市场系统特性分析及应用
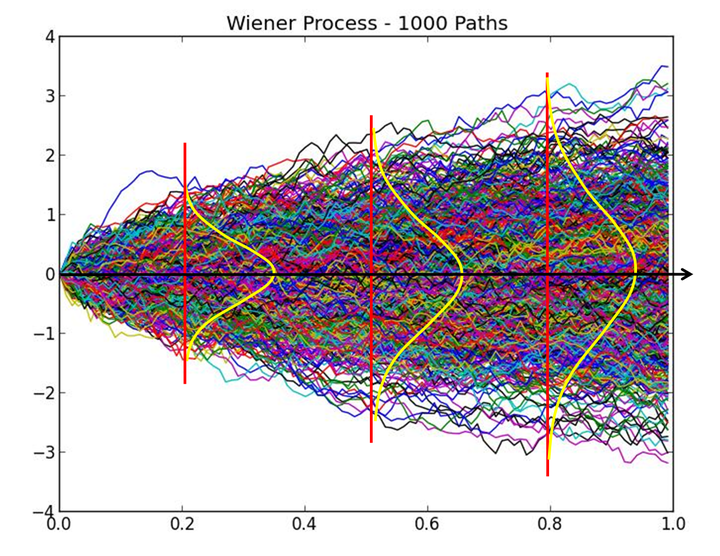
图1 布朗运动 标准差 不仅能度量大量布朗粒子偏离均值的发散程度,还能给出大量布朗粒子(样本轨道)位于 、 和 范围内的概率分别为68.3%、95.4%和99.7%。 图2为一个布朗粒子位移曲线的微分(瞬时速度),为服从 正态分布的高斯白噪声。因此,标准差 也可用来度量一个布朗粒子瞬时速度的大小。
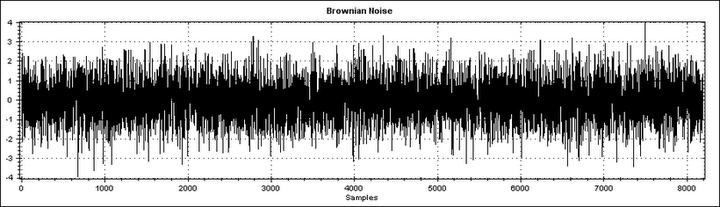
图2 布朗粒子瞬时速度 二)、波动率定义 图3为上证指数的日收益率,与图2所示的布朗粒子瞬时速度完全相似,为白噪声序列。将不同时刻的上证指数对数收益率作为样本点进行统计分析,其均值为0.0002,标准差 =0.02,最大波动幅度为±0.09,近似服从正态分布。
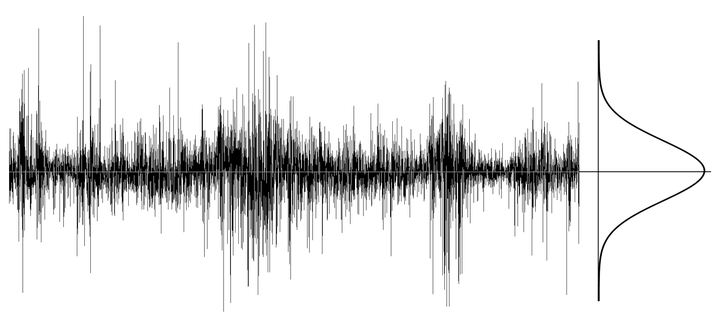
图3 上证指数收益率(日) 期权定价理论根据股票价格的收益率为白噪声序列的实证研究结果,建立了下面的下面的几何布朗运动模型 式中 为 时刻的股票价格, 为漂移率, 为波动率。 注意:期权定价理论错误地将股票价格 假设为随机变量,从式(3)的几何布朗运动模型得出了对数股票价格 服从正态分布的结论, 的方差为 期权定价理论将股票价格日收益率的标准差 定义为股票价格波动率,可根据式(4)计算出未来 时刻的股票价格波动程度 式中 为 时刻的股票价格波动率。 例如,上证指数日收益率的标准差 =0.02,按1年250个交易日计算,上证指数的年波动率(标准差)约为32%,也就是说,上证指数一年内在 %范围内波动的概率为68.3%,在 %范围内波动的概率为95.4%,在 %范围内波动的概率为99.7%。 三、波动范围与事实不符 根据式(5)的波动率计算公式,股票价格 未来 时刻在 范围内波动的概率为99.73%,这表明对数股票价格 的波动范围会随时间 的平方根不断增大,即 的波动范围会越来越大(图4)。